What is QLoRA?: A Visual Guide to Efficient Finetuning of Quantized LLMs

Sometimes smaller is better. How QLoRA combines efficiency and performance.

Get a list of personally curated and freely accessible ML, NLP, and computer vision resources for FREE on newsletter sign-up.

Consider sharing this with someone who wants to know more about machine learning.

---

In a previous article, we discussed how full fine-tuning large models such as GPT-4, Gemini, Claude, and LLAMA [2, 3, 4, 5, 6] for specific tasks is extremely resource (GPU and data) and capital-intensive.

LoRA or Low-Rank Adaptation came to the rescue as one of the most well-known methods for PEFT (Parameter-Efficient Fine-Tuning).

Can we get better than LoRA? Indeed QLoRA improves upon LoRA. A quote from the QLoRA paper:

“Our results show that QLoRA finetuning on a small high-quality dataset leads to state-of-the-art results, even when using smaller models than the previous SoTA.” [16]

In this visual guide, we discuss the technical details behind QLoRA, which is how it has become the default parameter-efficient fine-tuning method for LLMs.

Apple’s WWDC 2024 announcement [12] talks about quantization and LoRA being used for running large models (LLMs and MLMs [7]) directly on Apple devices to power their AI features (dubbed as “Apple Intelligence”).

“For on-device inference, we use low-bit palletization, a critical optimization technique that achieves the necessary memory, power, and performance requirements. To maintain model quality, we developed a new framework using LoRA adapters that incorporates a mixed 2-bit and 4-bit configuration strategy — averaging 3.7 bits-per-weight — to achieve the same accuracy as the uncompressed models. More aggressively, the model can be compressed to 3.5 bits-per-weight without significant quality loss.”

— Apple, June 2024

Today, we take a deep dive into QLoRA:

• Why should we care about methods such as LoRA and QLoRA?

• QLoRA vs. LoRA

• Primers on Floating Point Representations and Blockwise Quantization

• The NormalFloat4 Format

• Putting It All Together To Get QLoRA

• Final Thoughts and Takeaways

Would like to read other related pieces?
Here you can read more about the Transformers series and LLMs series.

---

[Jupyter Notebook] Build Your Own Open-source RAG Using LangChain, LLAMA 3 and Chroma

"Attention, Please!": A Visual Guide To The Attention Mechanism [Transformers Series]

---

1. Why should we care about methods such as LoRA and QLoRA?

By now, we know the basis of performant LLMs: pre-training.

The idea is to get similar performance without performing pre-training or full fine-tuning on large models.

Putting such a large volume of data with a model with trillions of parameters can cost over $100 million to train it (yes, this is ChatGPT4) across a cluster of 100-1000s of GPUs over a couple of weeks. Such pre-training runs are expensive and would only be performed every quarter or even annually.

— What is LoRA?: A Visual Guide to Low-Rank Approximation for Fine-Tuning LLMs Efficiently

Pre-training and fine-tuning are completely different beasts when it comes to resource intensiveness. For this reason, fine-tuning is run more frequently than a full pre-training.

2. QLoRA: Smaller Is Better

“We present QLoRA, an efficient finetuning approach that reduces memory usage enough to finetune a 65B parameter model on a single 48GB GPU while preserving full 16-bit finetuning task performance. QLoRA backpropagates gradients through a frozen, 4-bit quantized pretrained language model into Low Rank Adapters (LoRA)” [16]

QLoRA is weight quantization combined with LoRA. With the help of QLoRA models can be fine-tuned with the following benefits:

1. Lower Memory Requirements: The first thing that comes out of the box with quantization is a reduced memory footprint. Thanks to the quantization in QLoRA you can fine-tune bigger models than it would be possible with just regular fine-tuning (models with 33B and 65B parameters). The base model is quantized to store weights from 16 bits to 4 bits.

2. Competitive Performance: Fine-tuning with QLoRA results in performance competitive to that of a full-finetuning or LoRA fine-tuning.

3. Smaller is Better: QLoRA + smaller model + high-quality data performs better than previous SoTA that use larger models.

Of course, it also brings the benefits of the base LoRA which we mentioned in a previous post. Here is a summary but you can read all of this in more detail here:

1. Memory efficiency with <1% memory footprint: …

2. Converges to the performance of a fully fine-tuned model: …

3. No overhead during model inference: …

4. Time and cost-efficient fine-tuning: …

Before we jump into the technical details of the QLoRA, let’s first do a primer on how floating point numbers (weights in our case) are represented and stored.

---

Continue reading more:

The Challenges of Building Effective LLM Benchmarks

How Tesla Continuously and Automatically Improves Autopilot and Full Self-Driving Capability On 5M+ Cars

How Apple's iPhone Uses Private, On-Device Machine Learning To Recognize People In Photos

How Netflix Uses Machine Learning To Decide What Content To Create Next For Its 260M Users

Inside AlphaFold: DeepMind’s Recipe For Success

---

3. Floating Point Representations: A Quick Primer

To represent a floating point number in a binary format (FP32, FP16, TF32, etc.) one requires 3 pieces of information:

1. Sign: Is the number positive or negative? This is represented by a sign bit.

2. Range: How large of a number can this format support?

3. Precision: How finely can the format distinguish different values?

Different formats for floating point numbers.

The memory required to store each format depends on the number of bits the format needs to represent a number. Moreover, with the same number of bits, one can change the number of bits storing the range and the number of bits storing the precision.

Ideally, a good balance between range and precision should lead us to the ideal floating point format for machine learning. There has been empirical analysis on which floating point representation works best for machine learning:

“It has been empirically proven that the E4M3 is best suited for the forward pass, and the second version [E5M2] is best suited for the backward computation.” [19]

Let’s look at an example number and how it would be represented using 1 bit for the sign, 4 bits for the range, and 3 bits for the mantissa (the part after the decimal point).

-3.75 would be written as follows:

1. Sign: 1

2. Range: 0011

3. Precision: 110

Putting it together -3.75 is written as 10011.110

4. Blockwise Quantization: A Quick Primer

The paper mentions quantizing a 32-bit Floating Point (FP32) number to an Int8 which has a range [-127, 127]. Let’s go through this more concretely.

1. Define the 32-bit float tensor.

\(X_{FP32} = \begin{bmatrix} 0.1 & 0.2 & -0.1 & -0.5 & 0.7 & 0.8 & 0.9 & -1.0 \end{bmatrix} \)

2. Chunk the tensor into blocks. We use 2 blocks in this example.

   \(X_{FP32} = \begin{bmatrix} 0.1 & 0.2 & -0.1 & -0.5 \\ 0.7 & 0.8 & 0.9 & -1.0 \end{bmatrix} \)

3. Calculate the quantization constant for each block.

   \(\text{absmax}(X) = max(abs(X)) \)
   \(c_{FP32, \text{X}} = \frac{127}{absmax(X)}\)

   1. For block 1:

      \(\text{absmax} = 0.5 \)
      \(c_{FP32, \text{Block 1}} = \frac{127}{0.5} = 254\)

   2. For block 2:

      \(\text{absmax} = 1.0 \)
      \(c_{FP32, \text{Block 2}} = 127 \)

4. Quantize each block

   \(X_{Int8} = \text{round} \left( \frac{127}{\text{absmax}(X_{FP32})} \times X_{FP32} \right) = \text{round}(c_{FP32} \times X_{FP32}) \)

   1. For block 1:

      \(\begin{bmatrix} 0.1 & 0.2 & -0.1 & -0.5 \end{bmatrix} \)
      \(X_{Int8, \text{Block 1}} = \text{round}(254 \times \begin{bmatrix} 0.1 & 0.2 & -0.1 & -0.5 \end{bmatrix}) \)
      \(X_{Int8, \text{Block 1}} = \text{round}(\begin{bmatrix} 25.4 & 50.8 & -25.4 & -127 \end{bmatrix}) \)
      \(X_{Int8, \text{Block 1}} = \begin{bmatrix} 25 & 51 & -25 & -127 \end{bmatrix} \)

   2. For block 2:

      \(\begin{bmatrix} 0.7 & 0.8 & 0.9 & -1.0 \end{bmatrix} \)
      \(X_{Int8, \text{Block 2}} = \text{round}(127 \times \begin{bmatrix} 0.7 & 0.8 & 0.9 & -1.0 \end{bmatrix}) \)
      \(X_{Int8, \text{Block 2}} = \text{round}(\begin{bmatrix} 88.9 & 101.6 & 114.3 & -127 \end{bmatrix}) \)
      \(X_{Int8, \text{Block 2}} = \begin{bmatrix} 89 & 102 & 114 & -127 \end{bmatrix} \)

5. Combine quantized blocks

   \(X_{Int8} = \begin{bmatrix} 25 & 51 & -25 & -127 & 89 & 102 & 114 & -127 \end{bmatrix} \)

Here are the quantization constants:

\(c_{FP32, \text{Block 1}} = 254 \)

\(c_{FP32, \text{Block 2}} = 127 \)

What happens if we don’t use blockwise quantization?

Without blockwise quantization, information may be lost when large values are present in the input.

If the tensor being quantized has a large outlier value it will increase the absmax value. It is now possible that two values that are close but different can become indistinguishable after the quantization.

For simplicity, let’s say we have 3 numbers: [0.5, 3.0, 1000.0]. The absmax is now 1000.

Now let’s try to quantize them to Int8 (like above) with range [-127, 127].

\(\text{absmax} = 2000 \)

\(c_{FP32, X} = \frac{127}{2000} = 0.127\)

\(X_{Int8, \text{X}} = \text{round}(0.127 \times \begin{bmatrix} 0.5 & 3.0 & 1000 \end{bmatrix}) \)

\(X_{Int8, \text{X}} = \text{round}( \begin{bmatrix} 0.0635 & 0.381 & 127 \end{bmatrix}) \)

\(X_{Int8, \text{X}} = \begin{bmatrix} 0 & 0 & 127 \end{bmatrix} \)

Here, we can see that 0.5 and 3.0 both ended up being mapped to the same value i.e. 0 because of such a large quantization constant thanks to the outlier 1000.

5. The Need for A New Format: NormalFloat4 (NF4)

Standard quantization works well when the values are uniformly distributed in a range. If it is not that case standard quantization has a drawback.

“Since pretrained neural network weights usually have a zero-centered normal distribution” [16]

NormalFloat4 tackles this by assuming that the values to be quantized i.e. the values in X come from a normal distribution. The is taken and normalized by the absmax (max of the absolute values) so that the values now all fall between [-1, 1]. Now that we have our range of input values, let’s divide them into bins for quantization.

NormalFloat4 has 4-bits so we have 2^4 = 16 different bins available for quantization i.e. [0000, 0001, 0010, …, 1111]. Using standard quantization we could divide the range [-1, 1] into 16 equal-sized bins but we know that this is not ideal when values come from a normal distribution.

NF4 exploits the knowledge of the values following a normal distribution where a bulk of the values are around the center of the bell curve and then it flattens out at either extreme. With this QLoRA design NF4 creates bins based on the probability of finding points in that bin. Ideally, each bin has the same number of points falling in it assuring an optimal quantization.

Standard quantization is not optimal for data coming from the Normal distribution.

Quantile Quantization

Quantile Quantization is a technique used in data quantization where the goal is to ensure that each quantization bin has an equal number of values assigned from the input tensor. This is achieved by using the quantiles of the input data distribution.

1. Quantiles: Quantiles are points taken at regular intervals from the cumulative distribution function (CDF) of a random variable. For instance, the median is the 0.5 quantile, meaning 50% of the data is below this value.

2. Equal Bins: In quantile quantization, the input data is divided into bins in such a way that each bin contains an equal number of data points. This contrasts with standard (uniform) quantization, where bins have equal widths but might contain varying numbers of data points.

3. Optimal Data Type: Quantile quantization is considered information-theoretically optimal because it minimizes the quantization error by ensuring that the bins are populated equally, making efficient use of the available quantization levels.

Why is NF4 Optimal?

1. Error Minimization And Efficient Use of Bins: By ensuring an equal population of bins, NF4 minimizes quantization error, especially important for data with a normal distribution. Since each bin is equally populated, the NF4 data type makes efficient use of the available quantization levels, leading to better preservation of the original data's statistical properties.

2. Information-Theoretic Optimality: The process of quantizing based on quantiles is theoretically optimal because it distributes the quantization error evenly across the data range, rather than clustering errors in certain regions.

6. Intuition Behind QLoRA: Quantization + LoRA

QLoRA can fine-tune a quantized model without performance degradations.

Here is a step-by-step breakdown of what QLoRA does:

1. Quantize the model weights to their proposed NormalFloat4 (NF4) float format.

2. Train low-rank adapters on top of this.

“QLoRA reduces the average memory requirements of finetuning a 65B parameter model from >780GB of GPU memory to <48GB without degrading the runtime or predictive performance compared to a 16- bit fully finetuned baseline.” [16]

QLoRA is a success due to 3 main innovations that work in tandem to make it more efficient and equally performant to SoTA:

1. 4-bit NormalFloat Quantization: We converted this in the section above.

2. Double Quantization: This is the quantization of the quantization constant itself. For N blocks, there are N quantization constants. This step helps optimize memory footprint by quantizing these N values.

   “On average, for a blocksize of 64, this quantization reduces the memory footprint per parameter from 32/64 = 0.5 bits, to 8/64 + 32/(64 · 256) = 0.127 bits, a reduction of 0.373 bits per parameter.” [16]

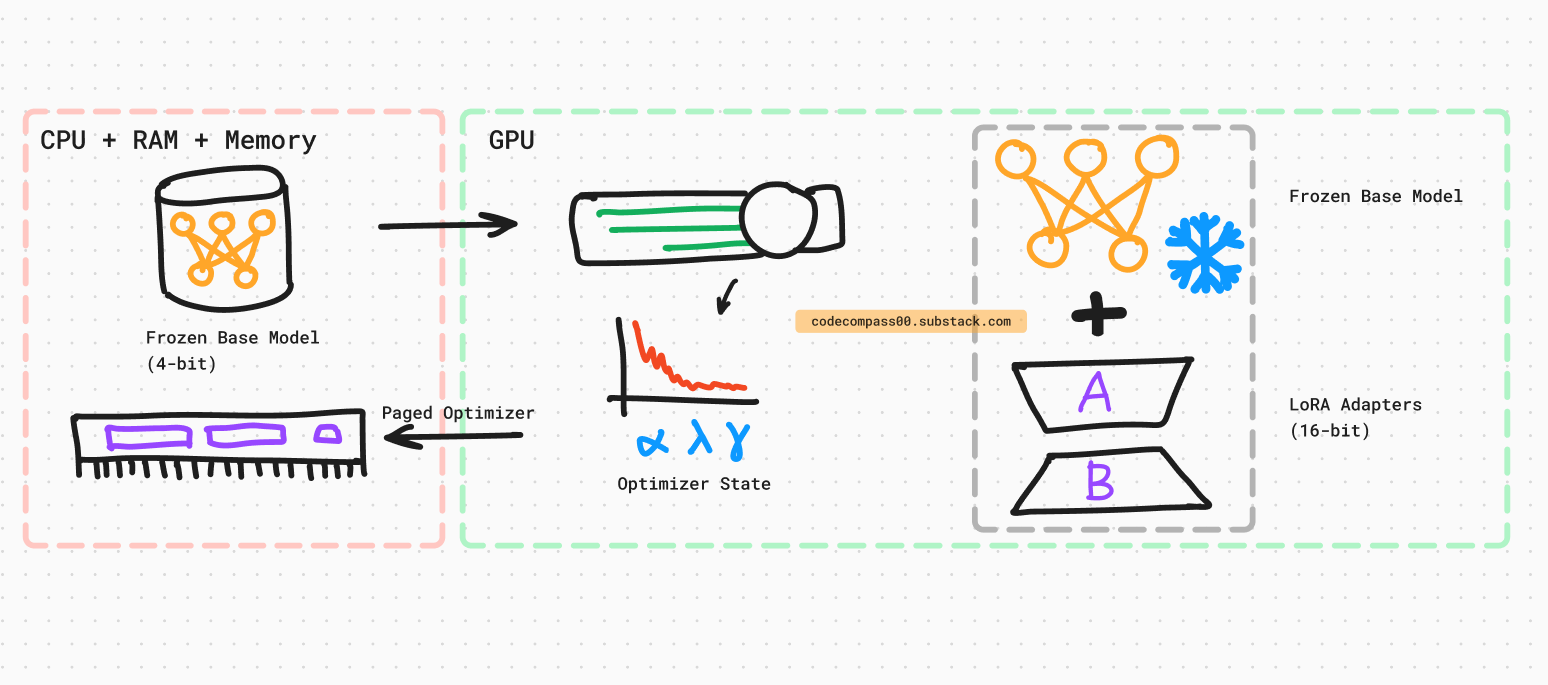
3. Paged Optimizers: When sequence lengths are extremely long, the GPU can run out of memory. To prevent this, optimizer states are moved from the GPU to the CPU. The optimizer state is moved back to the GPU for the optimizer’s update step.

   “… transfers between the CPU and GPU for error-free GPU processing in the scenario where the GPU occasionally runs out-of-memory” [16]

4. Quantization + LoRA: Tie the above together with low-rank adapters (see LoRA post for details).

These all tied together with low-rank adapters (LoRA) give a significant reduction in GPU memory consumption while maintaining performance.

Different pieces come together to make QLoRA efficient and perform better than the state-of-the-art in fine-tuning.

LoRA

Here is a quick summary. You can read more details about LoRA in the dedicated post.

What is LoRA?: A Visual Guide to Low-Rank Approximation for Fine-Tuning LLMs Efficiently

What is a Low-Rank Adapter?

A low-rank adapter consists of two smaller matrices, A and B, which are inserted into the model to capture task-specific variations. During training, only these matrices are updated, leaving the majority of the pre-trained model parameters unchanged.

\(W_{pretrained} = W_{pretrained} + \Delta W , \text{ where } W_{pretrained} \in \mathbb{R}^{M \times N}\)

Assume a matrix of the form MxN, with M=100 and N=100. LoRA “breaks” the MxN matrix down such that instead of updating 100*100 weights, only a small fraction of 10,000 parameters are involved in the process.

LoRA decomposes the matrix into 2 smaller matrices with fewer parameters than a full-blown matrix with MxN entries. To obtain the MxN matrix, A and B are multiplied.

Thanks to the quantization which reduced the memory footprint. With QLoRA, the number of low-rank adapters can be increased without increasing the memory significantly as most of the memory usage comes from storing the original (frozen) model weights and not so much from the LoRA parameters (weights) or their gradients.

Plot from [16] showing different parts and their GPU memory consumption.

“For a 7B LLaMA model trained on FLAN v2 with a batch size of 1, with LoRA weights equivalent to commonly used 0.2% of the original model weights, the LoRA input gradients have a memory footprint of 567 MB while the LoRA parameters take up only 26 MB.” [16]

What happens during training and inference?

QLoRA can be seen as using 2 data types:

• Storage Data Type: 4-bit NormalFloat (NF4). This is for the base model being fine-tuned which has its frozen weights quantized to NF4.

• Computation Data Type: 16-bit BrainFloat (BF16). When performing forward and backward passes, the storage data type is de-quantized (reverse of quantization) to 16-bit format. The 16-bit format is then used for computation.

Gradients are computed and applied only to the LoRA adapter parameters, which are also in 16-bit BrainFloat (BF16). The low-bit quantized weights are not updated directly during training. It is important to note that only LoRA parameters are updated.

7. Key Takeaways

1. 4-bit QLoRA with NF4 >> 16-bit LoRA

Using the NF4 format for quantization with QLoRA outperforms standard 16-bit finetuning as well as 16-bit LoRA.

NF4 with its quantization is more performant than FP16.

2. NormalFloat4 Format >> FloatingPoint4 Format

NF4 is more performant than the standard FP4 format. Double dequantization leads to minor performance gains but reduces memory footprint to fit larger models.

“Mean zero-shot accuracy over Winogrande, HellaSwag, PiQA, Arc-Easy, and ArcChallenge using LLaMA models with different 4-bit data types. The NormalFloat data type significantly improves the bit-for-bit accuracy gains compared to regular 4-bit Floats. While Double Quantization (DQ) only leads to minor gains, it allows for a more fine-grained control over the memory footprint to fit models of certain size (33B/65B) into certain GPUs (24/48GB).” [16]

3. Increase Params + Reduce Precision

Given a constant budget, it is better to increase the number of parameters and decrease their precision.

“… with a given finetuning and inference resource budget it is beneficial to increase the number of parameters in the base model while decreasing their precision” [16]

4. Data Quality >> Data Size

One of the most important takeaways from the paper is that data quality >> data size!

“… we find that data quality is far more important than dataset size, e.g., a 9k sample dataset (OASST1) outperformed a 450k sample dataset (FLAN v2, subsampled) on chatbot performance, even when both are meant to support instruction following generalization.” [16]

See you in the next edition of the Code Compass.

Read more on the Transformers series, LLMs series, or Tesla’s data engine:

How Tesla Continuously and Automatically Improves Autopilot and Full Self-Driving Capability On 5M+ Cars

---

Consider subscribing to get it straight into your mailbox:

References

• [1] Attention Is All You Need: https://arxiv.org/abs/1706.03762

• [2] GPT-4 Technical Report: https://arxiv.org/abs/2303.08774

• [3] Gemini: A Family of Highly Capable Multimodal Models: https://arxiv.org/abs/2312.11805

• [4] Gemini 1.5: https://arxiv.org/abs/2403.05530

• [5] Claude 3: https://www.anthropic.com/news/claude-3-family

• [6] LLAMA: https://arxiv.org/abs/2302.13971

• [7] Multimodal Large Language Models: A Survey

• [8] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale: https://arxiv.org/abs/2010.11929

• [9] Intro to Large Language Models: youtube.com/watch?v=zjkBMFhNj_g

• [10] Hugging Face LoRA: https://huggingface.co/docs/diffusers/training/lora

• [11] LoRA: Low-Rank Adaptation of Large Language Models: https://arxiv.org/abs/2106.09685

• [12] Apple WWDC 24: https://developer.apple.com/wwdc24/

• [13] Mistral: https://mistral.ai/

• [14] Matrix rank: https://en.wikipedia.org/wiki/Rank_(linear_algebra)

• [15] Pytorch: https://pytorch.org/

• [16] QLoRA: Efficient Finetuning of Quantized LLMs: https://arxiv.org/abs/2305.14314

• [17] Floating point representation: Wikibook

• [18] Transformers: QLoRA + bitsandbytes

• [19] Transformers: bitsandbytes