What is LoRA?: A Visual Guide to Low-Rank Approximation for Fine-Tuning LLMs Efficiently
Why LoRA Is Essential For Model Fine-Tuning
Get a list of personally curated and freely accessible ML, NLP, and computer vision resources for FREE on newsletter sign-up.
Consider sharing this with someone who wants to know more about machine learning.
Fine-tuning large language models (LLMs) like GPT-4, Gemini, Claude, and LLAMA [2, 3, 4, 5, 6] for specific tasks is resource-intensive. LoRA [11] (Low-Rank Adaptation) offers an efficient solution, reducing the computational and financial costs associated with traditional fine-tuning methods. This visual guide explains how LoRA works and why it's crucial for optimizing LLMs.
In this visual guide, we go over the technical details behind LoRA and why in practice it is one of the most well-known methods for PEFT (Parameter-Efficient Fine-Tuning)
Even Apple’s latest WWDC 2024 announcement [12] talks about LoRA running large models (LLMs and MLMs [7]) directly on devices (iPhones, Macs, and iPads) to power their AI features (dubbed as “Apple Intelligence”) thanks to the efficiency and performance of LoRA. But let’s leave that for another time and jump head-first into understanding LoRA.
Today, we take a deep dive into LoRA:
What is fine-tuning and why does your LLM need it?
Drawbacks of Previous Fine-Tuning Methods
How does LoRA Fit into LLM Fine-tuning?
Intuition Behind LoRA: Parameter Efficient Fine-tuning
How does LoRA work and what are its practical implications?
What does it look like in practice? With the help of a Python example.
Would like to read other related pieces?
Here you can read more about the Transformers series and LLMs series.
1. What is fine-tuning and why does your LLM need it?
By now, we know the basis of performant LLMs: pre-training. Models are shown substantial portions of the internet to build a highly detailed internal representation of this data. This data is in the order of 10s of TB (terabytes) of text files. Putting such a large volume of data with a model with trillions of parameters can cost over $100 million to train it (yes, this is ChatGPT4) across a cluster of 100-1000s of GPUs over a couple of weeks. Such pre-training runs are expensive and would only be performed every quarter or even annually. [9]

Fine-tuning comes right after pre-training. It involves a relatively smaller scale of operations and has very specific, targeted data that we want to show the model. The idea is to curate a very high-quality fine-tuning dataset. The goal of fine-tuning is to make this “generalist” pre-trained model more specialized. For example, in the case of ChatGPT, it is the idea to be a helpful assistant.
2. Drawbacks of Traditional Fine-Tuning Methods
Before LoRA, fine-tuning methods (a form of transfer learning) typically involved updating a large number of parameters. This approach, while effective, had significant drawbacks:
Computational Cost: Fine-tuning large models like GPT-4 involves updating billions (even trillions) of parameters, requiring substantial computational power and memory.
Training Time: The extensive parameter updates increase the training time, making the process slow.
Resource Intensity: High resource usage translates to increased financial costs, which can be prohibitive for many practitioners.
Continue reading more:
3. Why LoRA? How It Fits into LLM Fine-tuning
LoRA addresses these challenges by using low-rank adaptation, which focuses on efficiently approximating weight updates. This significantly reduces the number of parameters involved in fine-tuning.
With this simple idea but powerful idea, LoRA can help in efficient model tuning also known as PEFT. LoRA comes with these advantages over other methods especially the full fine tuning (which would have the ability to update all the possible model parameters if the optimizer told it to):
Memory efficiency with <1% memory footprint: LoRA is able to reduce the parameters to be updated to a small fraction of the number of parameters in the model. This can vary on the implementation but the paper shows that <1% of the weights are required to be adapted when using LoRA.
Converges to the performance of a fully fine-tuned model: Even with tuning just <1% of the model weights the model trained with LoRA is competitive and converges to a model that is fully fine-tuned i.e. all of its weights are updated. LoRA provides the same performance as if it were fully fine-tuned (without freezing any weights).
No overhead during model inference: During inference time no additional setup is required to construct the model.
Time and cost-efficient fine-tuning: Since only a fraction of the parameters are “trained” the benefits of a fully fine-tuned model can be realized at the fraction of the GPUs, time, and $$$ (€€€ if you are Mistral [13]) that would be required to perform a round of full fine-tuning.
4. Intuition Behind LoRA: Parameter Efficient Fine-tuning
LoRA addresses these challenges by using low-rank adaptation, which focuses on efficiently approximating weight updates. This significantly reduces the number of parameters involved in fine-tuning.
Let’s take a step back. What do model weight updates even look like?
Model training (LLMs or other architectures) and fine-tuning involve updating matrices that hold the parameters of all the different layers in the model.
Assume a matrix of the form MxN, with M=100 and N=100. LoRA “breaks” the MxN matrix down such that instead of updating 100*100 weights, only a small fraction of 10,000 parameters are involved in the process.

5. How does LoRA work?
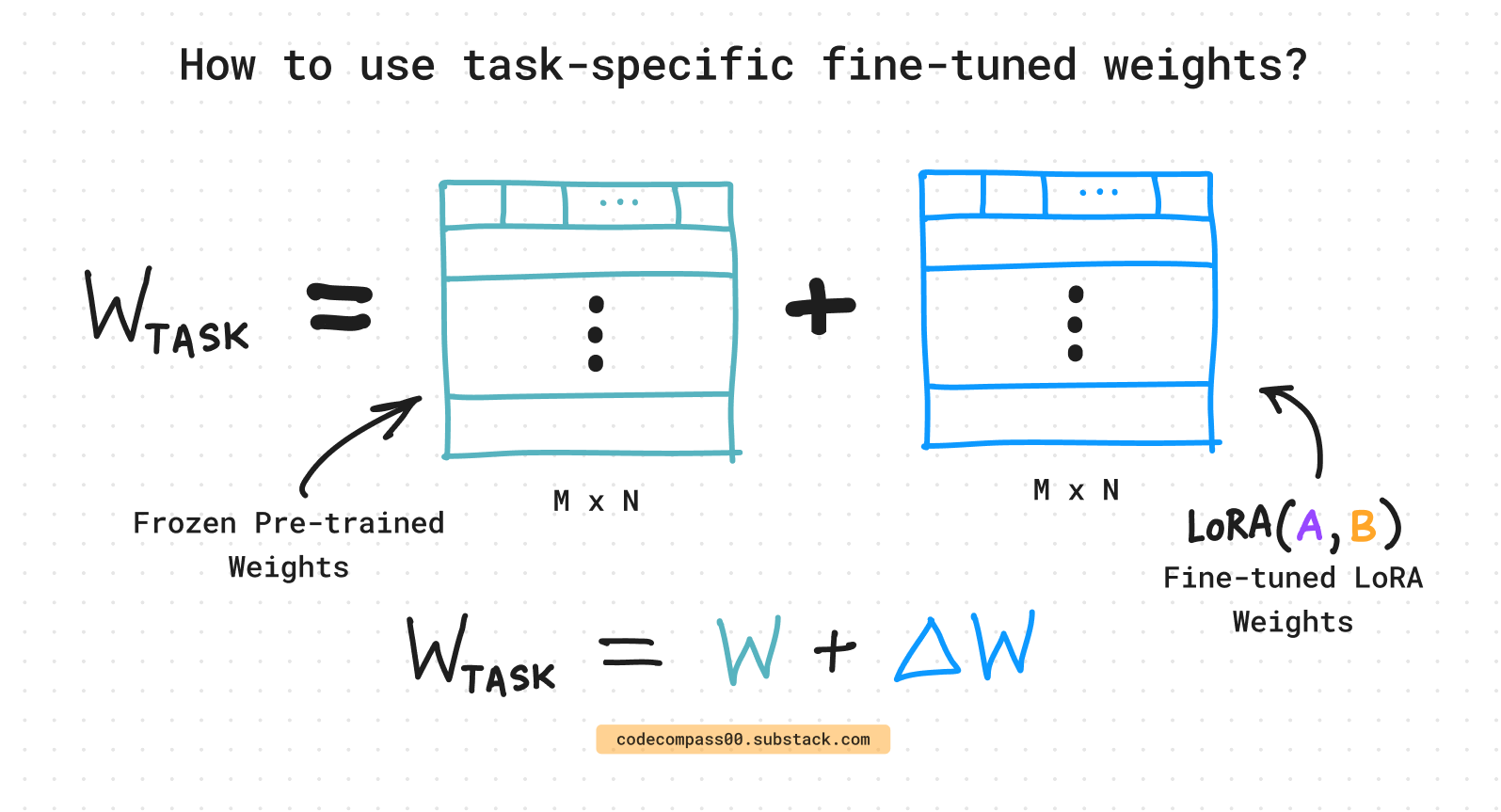
LoRA introduces two low-rank [14] matrices, A and B, to approximate weight updates. Instead of directly updating the weight matrix W, LoRA approximates the update using the product of A and B:
Here, A and B are much smaller than the original weight matrix W, reducing computational complexity.
What is a Low-Rank Adapter?
A low-rank adapter consists of two smaller matrices, A and B, which are inserted into the model to capture task-specific variations. During training, only these matrices are updated, leaving the majority of the pre-trained model parameters unchanged.
5. Why does LoRA need to fine-tune only <1% of the total model parameters?
Imagine one of the weight matrices in the pre-trained model W. W has M=1000 and N=1000. This matrix has M*N = 1,000,000 floating point weights or model parameters.
Now, during full-fine tuning, all 1,000,000 weights would be updated by adding an update matrix (delta W) also containing 1,000,000 weights. Let’s take note of this.
Full fine-tuning: 1,000,000 weights to “learn”
With LoRA, we break delta W into a product of 2 smaller matrices, A and B.
A has the shape Mxr and B has the shape rxN. r is chosen to be smaller than M and N.
In our toy example, let’s choose r to be 5.
A has M*r weights i.e. 1000*5 = 5,000.
B has r*N weights i.e. 1000*5 = 5,000.
LoRA fine-tuning: 5,000 + 5,000 = 10,000 weights to “learn”
In LoRA, we multiply these 2 matrices to get a delta W which has a shape that matches the pre-trained matrix W with MxN.1 That way we can use this to update the pre-trained matrix W but with a fraction of the parameters (depending on the choice of r, of course).
Fraction of weights when using LoRA instead: 10,000/1,000,000 = 1%

6. Practical Implications of LoRA
Deploy multiple models: Single pre-trained model base + Multiple LoRA adapters
Imagine having multiple tasks to solve on a low-powered device. Think of solving tasks such as text summarization, text tone adjustment, question-answering, math, and language tutoring on a compute-limited iPhone if you are Apple. Apple could deploy multiple foundational models but instead, they could have a single pre-trained base and have separate, task-specific LoRA adapters.
Think of the LoRA adapters as costumes that the foundational model can wear to become what it wants: Batman, Wolverine, Wonder Woman, or Hulk.
The base pre-trained model can be frozen with the LoRA layers ready to be swapped in and out based on the task at hand.
Data Requirements for Fine-Tuning
The amount of data required for fine-tuning depends on the specific task and the complexity of the model. Generally, fine-tuning requires significantly less data than pre-training. While pre-training might involve billions of tokens, fine-tuning can be effective with thousands of labeled examples. The quality and relevance of the fine-tuning data are crucial for achieving good performance.
Performance and Cost Benefits
LoRA offers significant gains in training time and cost. By reducing the number of parameters to update, LoRA allows models to be fine-tuned faster and with less computational power, making it accessible to more practitioners.
LoRA in the Context of PEFT
LoRA is an example of Parameter-Efficient Fine-Tuning (PEFT), a broader category of techniques aimed at making fine-tuning more efficient. Other PEFT methods include adapter modules, prefix tuning, and prompt tuning. Each method has its own advantages and trade-offs.
For more information on PEFT, refer to Hugging Face's PEFT documentation.
7. How does LoRA behave during training and inference?
During Training
Initialization: Initialize matrices A and B with random values.
Forward Pass: During each forward pass, compute the low-rank approximation as A×B and add this to the original weights.
Backward Pass: Only update A and B during backpropagation.
During Inference
Inference: During inference, the product A×B is precomputed and added to the original weights, ensuring the model operates efficiently without needing to recompute the low-rank approximation repeatedly.
8. What does LoRA look like in practice?: A Python Toy Example
Here is a snippet in Python using Pytorch [15] that computes attention:
import numpy as np
class LoRA:
def __init__(self, weight_shape: tuple[int, int], rank: int,
learning_rate: float = 0.01) -> None:
"""
Initialize the LoRA class with weight matrix dimensions, rank,
and learning rate.
Parameters:
- weight_shape: tuple, the shape of the original weight matrix
(m, n)
- rank: int, the rank for the low-rank approximation
- learning_rate: float, learning rate for the update
"""
self.weight_shape = weight_shape
self.rank = rank
self.learning_rate = learning_rate
m, n = weight_shape
self.A: np.ndarray = np.random.randn(m, rank)
self.B: np.ndarray = np.random.randn(rank, n)
def forward(self, W_pretrained: np.ndarray) -> np.ndarray:
"""
Perform the forward pass using LoRA.
Parameters:
- W_pretrained: numpy array, the original weight matrix of shape
(m, n)
Returns:
- W_prime: numpy array, the adapted weight matrix
"""
delta_W: np.ndarray = np.dot(self.A, self.B)
W_prime: np.ndarray = W_pretrained + delta_W
return W_prime
def training_step(self, grad_A: np.ndarray, grad_B: np.ndarray) -> None:
"""
Perform a single training step for LoRA.
Parameters:
- grad_A: numpy array, gradient for low-rank matrix A
- grad_B: numpy array, gradient for low-rank matrix B
"""
# Update A and B using the provided gradients
self.A -= self.learning_rate * grad_A
self.B -= self.learning_rate * grad_B
def reconstruct(self) -> np.ndarray:
"""
Reconstruct the full weight matrix from the low-rank adaptation.
Returns:
- delta_W: numpy array, the low-rank approximation of the weight
update
"""
delta_W: np.ndarray = np.dot(self.A, self.B)
return delta_WOnce we have the above setup, we can simulate how it would look like.
# Original weight matrix
W_pretrained: np.ndarray = np.random.randn(4, 4)
rank: int = 2 # Low-rank approximation rank
lora: LoRA = LoRA(W_pretrained.shape, rank)
# Perform a forward pass
W_prime: np.ndarray = lora.forward(W_pretrained)
print("Adapted weight matrix W_prime:\n", W_prime)
# Simulate gradients for A and B.
# In practice, these come from backpropagation.
grad_A: np.ndarray = np.random.randn(*lora.A.shape)
grad_B: np.ndarray = np.random.randn(*lora.B.shape)
# Perform a training step.
lora.training_step(grad_A, grad_B)
print("Updated low-rank matrices A and B:\n", lora.A, "\n", lora.B)
# Reconstruct the low-rank approximation.
delta_W: np.ndarray = lora.reconstruct()
print("Low-rank approximation delta_W:\n", delta_W)9. Looking Ahead: What’s next?
While LoRA is a powerful technique, the field of fine-tuning is continuously evolving with new methods being developed. Other techniques such as adapter modules, prefix tuning, and prompt tuning offer different approaches to fine-tuning LLMs efficiently. The more recent Q-LoRA [16] combines LoRA with quantization to unlock quantization-aware fine-tuning. Before I leave, here is a quote from the Q-LoRA paper:
“Our results show that QLoRA finetuning on a small high-quality dataset leads to state-of-the-art results, even when using smaller models than the previous SoTA.” [16]
See you in the next edition of the Code Compass.
Read more on the Transformers series, LLMs series, or Tesla’s data engine:
Consider subscribing to get it straight into your mailbox:
References
[1] Attention Is All You Need: https://arxiv.org/abs/1706.03762
[2] GPT-4 Technical Report: https://arxiv.org/abs/2303.08774
[3] Gemini: A Family of Highly Capable Multimodal Models: https://arxiv.org/abs/2312.11805
[4] Gemini 1.5: https://arxiv.org/abs/2403.05530
[5] Claude 3: https://www.anthropic.com/news/claude-3-family
[6] LLAMA: https://arxiv.org/abs/2302.13971
[8] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale: https://arxiv.org/abs/2010.11929
[9] Intro to Large Language Models: youtube.com/watch?v=zjkBMFhNj_g
[10] Hugging Face LoRA: https://huggingface.co/docs/diffusers/training/lora
[11] LoRA: Low-Rank Adaptation of Large Language Models: https://arxiv.org/abs/2106.09685
[12] Apple WWDC 24: https://developer.apple.com/wwdc24/
[13] Mistral: https://mistral.ai/
[14] Matrix rank: https://en.wikipedia.org/wiki/Rank_(linear_algebra)
[15] Pytorch: https://pytorch.org/
[16] QLoRA: Efficient Finetuning of Quantized LLMs: https://arxiv.org/abs/2305.14314
It is always a good rule of thumb to make sure your matrix shapes are matching and look at them to understand better what is happening under the hood.