What are 1x1 Convolutions in CNNs?
Learn what 1x1 convs are and how to build lightweight and performant CNNs
Get a list of personally curated and freely accessible ML, NLP, and computer vision resources for FREE on newsletter sign-up.
1x1 convolutions are a powerful tool when designing convolutional neural network (CNN) architectures for your task. We'll go over what 1x1 convolutions are, how they work, and why you should consider using them in your next project.
To read more on this topic see the references section at the bottom. Consider sharing this post with someone who wants to study machine learning.
What do 1x1 convolutions help you achieve?
By incorporating 1x1 convolutions into your CNN architecture, you can achieve:
Reduced model size: Smaller models require less memory with faster training and inference.
Improved efficiency: Less computation is needed for processing data.
Deeper models: The parameter budget that you saved can be reallocated to build deeper, more performant models [3].
Convolution filtered in deep learning. [6]
Are you looking to understand convolutions in deep learning better? Check out this excellent visual guide to convolutions [6].
What are 1x1 convolutions?
1x1 convolutions offer a powerful way to improve CNN efficiency. Instead of detecting spatial features, it combines information across channels in the input feature volume.
1x1 convolutions are siblings of the pooling layer. Let’s see where they differ and where they are similar.
A 2x2 max pool aggregates across the spatial dimensions H and W. It would take an input feature from (N, C, H, W) to (N, C, H/2, W/2).
A 1x1 convolution aggregates across the channel dimension C. It can take an input feature from (N, C, H, W) to (N, C’, H, W)1. It is a channel-wise weighted pooling, learning relationships across the channel dimensions of the feature volume.
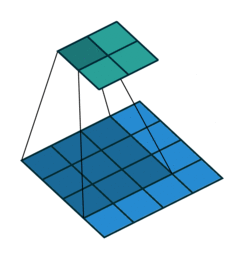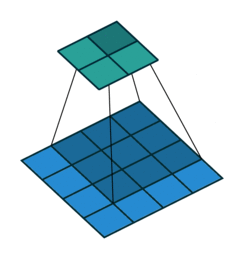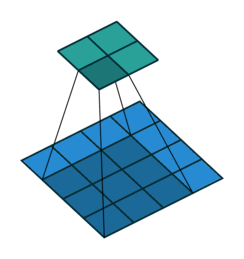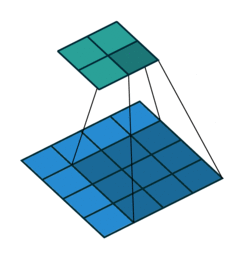
Visualizing 1x1 convolutions
We have 5x5 spatial locations and 6 channels in the input feature volume. The 1x1 convolution has a filter with 6 channels to match the 6 channels in the input. It has a 1x1 spatial dimension meaning.
The output volume at (x, y) takes the value of the dot product of all channels at (x, y) in the input and the convolution filter. Repeat this for all spatial locations to get the complete output feature map with 1 channel with 5x5 spatial dimensions. Note how both the input and the output maintain the spatial resolution of 5x5 but the channels change from 6 to 1.
Continue reading more:
!["Attention, Please!": A Visual Guide To The Attention Mechanism [Transformers Series]](https://substackcdn.com/image/fetch/w_140,h_140,c_fill,f_webp,q_auto:good,fl_progressive:steep,g_auto/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F375dc525-fa19-4e6f-81f2-68820bfd36a1_1903x856.png)
Reducing Parameters and Boosting Efficiency
One of the biggest advantages of 1x1 convolutions is their ability to reduce the number of parameters in your model. Here's how:
Traditional convolutions with large filters require numerous parameters.
1x1 convolutions act as a bottleneck, reducing the number of channels before feeding them into computationally expensive operations like larger convolutions with 5x5 and 7x7 filters2.
This translates to a model with a smaller memory footprint and faster training and inference times. This makes it a perfect use case for models meant to run on edge and mobile devices.
Achieving parameter efficiency with 1x1 convolutions: A Numerical Example
Modern neural network architectures consist of multiple repeated blocks of computation. Consider a block that takes a 100 x 20 x 20 feature volume as input and outputs a 40 x 20 x 20 feature volume. Here are 2 possible variants to achieve this. Let’s look at it visually.